The Mathematical Practices Are the Metacognition Our Kids Need

Support for metacognition in the mathematics classroom often looks like either a lot of teacher-led modeling and thinking out loud or giving students loads of problems to solve in the hope that they will somehow discover the most useful approaches and strategies on their own.

Most teachers will tell you that in practice, neither of these approaches works very well. And they really don’t work for students who are already struggling. According to William Emeny, for many students, it’s better to “show them the [metacognitive] toolkit and teach them how to use it one tool at a time…teaching one’s brain to control the thought processes it has for the purpose of directing it towards the management of their own learning.”

The Value of Fostering Metacognition in Mathematics

Why metacognition ? Plain and simple, it elevates student achievement. Recent research has shown that students who were taught metacognitive strategies made an average of eight months more progress than students who were not. And that, according to Emeny, was over the course of just one year.

It also supports student ownership of mathematics. When students hit difficult math problems that leave them feeling frustrated — it can be tempting for them to give up and resort to the words “I can’t do it.” That’s why it is important for teachers to support and model the metacognitive process. Asking questions gets the metacognitive work going internally so that students begin to gain conceptual understanding and procedural skill and fluency while applying what they have learned. Encouraging students to talk about their learning stimulates their thinking about their thinking. In short, it fosters their mathematical metacognition. The more students are able to understand their own learning process and articulate it, the easier it will be for them to figure out what strategies and supports work best for them — skills that transfer across content areas and life — the skills of student ownership.

Fostering metacognition in mathematics requires a balance of explicit instruction, teacher modeling, student-centered exploration, and responsive coaching that helps students first learn the kinds of questions and thought processes they can apply, and then grow to use them on their own. In other words, it takes an intentional instructional approach with a gradual release of responsibility to support students to think like a mathematician and speak like one too. These metacognitive skills come naturally to some students but not to others. Therefore, teachers must play an active role in teaching them and helping students own their mathematical learning.

Metacognition and the Strands of Math Proficiency

Larson and Kanold suggest that for too long, judgments about what constitutes “good” math instruction have been based on false dichotomies. Learning is either student-centered or teacher-directed, and its goal either conceptual understanding or procedural fluency. Both of these either/or propositions vastly oversimplify the complexity of what our brains need to know and to do to engage in mathematical thought.

Indeed, the influential report of the National Mathematics Advisory Panel found that “all-encompassing recommendations that instruction should be entirely ‘student-centered’ or ‘teacher-directed’ are not supported by research,” and that “the curriculum must simultaneously develop conceptual understanding, computational fluency, and problem solving skills.”

That report underscored the key findings of another seminal report from the National Research Council (NRC), Adding It Up: Helping Children Learn Mathematics, which found that, much like literacy, attaining proficiency in math requires learners to weave together multiple strands all at once. These key strands of mathematical proficiency drew on and further refined mathematical process standards that had been developed over the previous two decades by the National Council of Teachers of Mathematics (NCTM).

The Common Core State Standards for Mathematics brought together this vast array of research and instructional expertise to present a clear framework for metacognition in mathematics by placing a strong emphasis on the equal importance of procedural skill and mathematical understanding. And, they are clear in what they mean by mathematical understanding.

“One hallmark of mathematical understanding is the ability to justify, in a way appropriate to the student’s mathematical maturity, why a particular mathematical statement is true or where a mathematical rule comes from. There is a world of difference between a student who can summon a mnemonic device to expand a product such as (a + b)(x + y) and a student who can explain where the mnemonic comes from. The student who can explain the rule understands the mathematics, and may have a better chance to succeed at a less familiar task such as expanding (a + b + c)(x + y).”

Knowing this, it is easy to see why the math standards incorporated standards of two very different types, the Standards for Mathematical Content and the Standards for Mathematical Practice. By articulating both content and practice, the standards define both what students should know and be able to do in mathematics and how they should be thinking about mathematics.

Defining the Practices for Metacognition

The Standards for Mathematical Practice grew out of the NCTM process standards as well as the NRC strands of proficiency. They acknowledge that weaving together all of the strands of mathematical proficiency is a complex process that requires students to acquire both content knowledge as well as a variety of skills and practices.

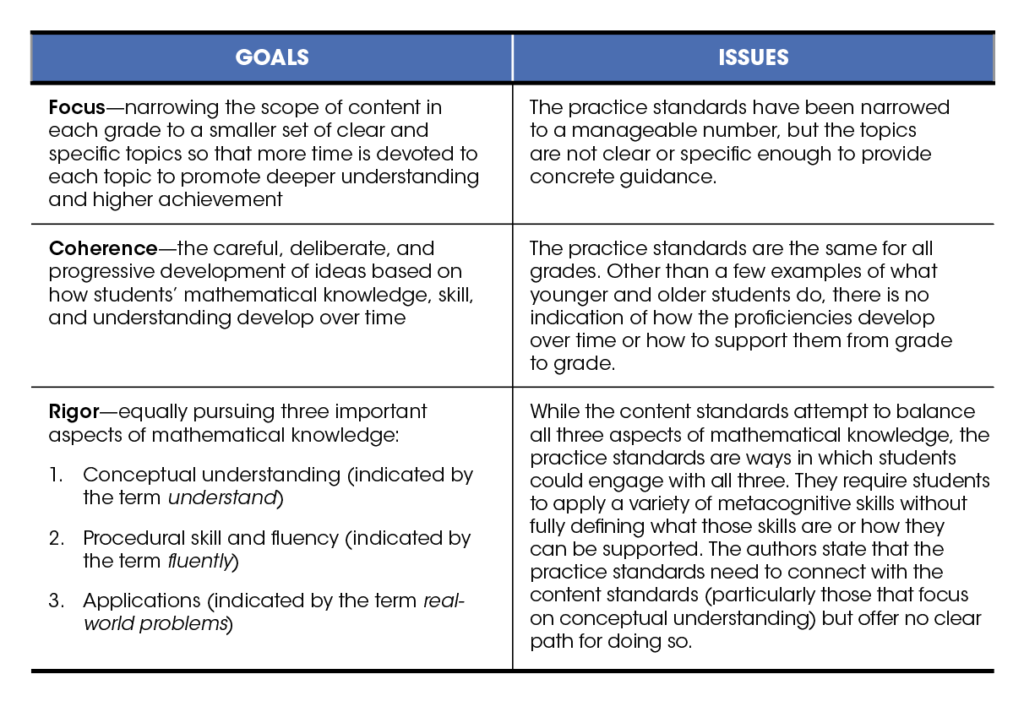
The Standards for Mathematical Practice present a helpful framework for this complex and important work. They are the same for all grade levels and represent ways that students can engage with mathematics. A few examples are included of how students at different levels or studying different topics might apply or demonstrate the proficiencies described.

But, while these brief descriptions are helpful for figuring out what the standards mean, they are not specific enough to provide much practical guidance for classroom implementation. In short, the practice standards lack the elements of focus, coherence, and rigor that the standards as a whole were created to achieve. In order to bring clarity around each element as they relate to the practice standards, let’s examine the goals and issues for each.

As teachers, helping students do this cognitive work can feel as complex as the work the students themselves are doing. We need to understand:

• the value of the two types of standards themselves,
• how the standards progress from kindergarten to high school, and
• how to teach the processes involved when students are learning the skills within the standards.

If we can do these three things and provide resources to our parents and caregivers so they can support mathematical metacognition at home, we will be helping our students the necessary conceptual understandings as well as the procedural and metacognitive skills required to be successful with math.